2007年3月18日「爭取普選改善民生」遊行人數點算計劃返回

2007年3月18日「爭取普選改善民生」遊行人數點算計劃

「2007年3月18日『爭取普選改善民生』遊行人數點算計劃」由香港大學民意研究計劃主任鍾庭耀獨立進行，作為一項義務社會服務。點算結束後，數據首先以新聞公報方式發佈，然後於翌日上載至本網頁。

點算總結

香港香港大學民意研究計劃主任鍾庭耀，今日下午在灣仔軒尼詩道與軍器廠街交界行人天橋上點算由民間人權陣線和泛民立法會議員發起的「爭取普選改善民生大遊行」人數，估計總人數介乎4,000至4,700人之間。

民研計劃是採用多年來慣用的方法，把上述軒尼詩道地段的行車路面橫切成為兩條行人路線，再按時段抽樣點算個別路線的人數，然後合計經過該路段的總人數，再根據過往調查紀錄調整中途插隊或離隊的人數，得出估計數字。

不過，由於參與是次遊行人數明顯少於過往同類活動，警方又在上述點算地點附近四次截流，每次約一分鐘，因此，民研計劃主任今次採用了比較密集的點算程序，再結合警方截流的情況，進行統計。以下是分段分線的點算和統計：

開始時間結束時間第一行車線第二行車線備註合計

1649          龍頭到達

1649 1652 409 全麵點算，包括一分鐘截流 409

1652 1654 每分鐘259    共2分鐘 1036

1654 1655 每分鐘123       246

1655 1657 每分鐘94    共2分鐘 376

1657 1659    每分鐘146 共2分鐘 584

1659 1700    每分鐘69    138

1700 1701 －－警方截流，人流沒有前進 0

1701 1702    每分鐘148    296

1702 1703 －－警方截流，人流沒有前進 0

1703 1706    152 全麵點算第二行車線，包括截流時間；龍尾於1706經過 304

1649 1706 經過點算地點總人數 3,389

上述數據顯示，從遊行龍頭抵達起至龍尾經過為止，估計有3,389人經過與軍器廠街交界的行人天橋底，但有關數字並未包括在該點之前離隊或之後插隊的遊行人士。民研計劃因此引用2005年12月4日「爭取普選」遊行人數點算計劃得出的調整參數，即1.18至1.38，作為調整的基礎。換言之，參與今日遊行的總人數估計是介乎4,000至4,700之間。

有關2005年12月4日的遊行人數點算方法，請參閱《香港大學民意網站》(http://hkupop.pori.hk)中「遊行集會研究專頁」之「香港大學學生研究隊2005年12月4日『爭取普選』遊行人數點算計劃」。

點算方法

點算地點：灣仔軒尼詩道與軍器廠街交界行人天橋（進入金鐘地段）
點算工具：手動點算器、計時器、計數機、記錄表
點算時間：人流在1649至1706之間經過該點

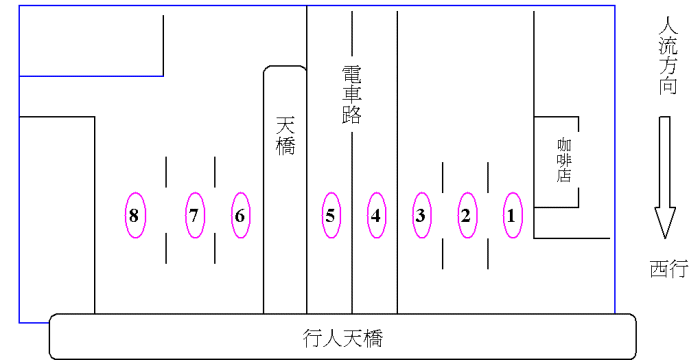
路面示意圖：

由於人數有限，警方只開放1及2號行車線作遊行用途。民意研究計劃主任於是在不同時段點算1及2號行車線的經過人數，再結合警方截流的情況，計算人數。

統計方法

假設在某一時段的P1分鐘內，遊行人士通過路線1的速度為每分鐘Y1人，則在該時段內從路線1經過該點的人數為（P1‧Y1）人。同樣道理，如果人流在同期通過路線2的速度為每分鐘Y2人，則在該時段內從路線2經過該點的人數為（P1‧Y2）人......餘此類推。同期通過2條路線的人數則為（P1‧Y1）＋（P1‧Y2），而全日通過2條路線的人數則為：P1時段所有人數＋P2時段所有人數＋……餘此類推，直至遊行遊行人士全部通過該點為止。全日參加遊行的總人數＝經過該點的人數＋沒有經過該點的人數（包括中途插隊或離隊人士），需要倚靠其他方法作出估計。

由於參與是次遊行人數明顯少於過往同類活動，民研計劃因此不打算透過全港巿民抽樣調查來計算調整參數，而是使用2005年12月4日「爭取普選」遊行人數點算計劃得出的調整參數，即1.18至1.38，作為調整的基礎，計算出遊行總人數為介乎4,000至4,700之間，具體計算方法如下：

民研計劃在2005年12月9至2006年1月20日期間，進行了多次隨機抽樣電話調查，找到225名曾參與2005年12月4日「爭取普選」遊行的巿民，當中78.6%謂曾經通過當時的點算地方，而在95%置信水平下，讀數78.6%的純抽樣誤差為正負6個百分比。以同樣調整參數計算2007年3月18日「爭取普選改善民生」，可以得出以下結果：


	上限 ＝ 3,389 x (100 / (78.6 - 6.1) ) = 4,674

	平均 ＝ 3,389 x (100 / 78.6) = 4,312

	下限 ＝ 3,389 x (100 / (78.6 + 6.1) ) = 4,001

即大約介乎4,000至4,700之間。